
Available online at (accessed May 14, 2013). Data from the National Basketball Association.Available online at en./wiki/List_o.ms_by_capacity (accessed May 14, 2013). “List of stadiums by capacity.” Wikipedia.Data from The World Almanac and Book of Facts.Available online at nces.ed.gov/programs/digest/d.s/dt09_147.asp (accessed May 14, 2013). “Digest of Education Statistics: ACT score average and standard deviations by sex and race/ethnicity and percentage of ACT test takers, by selected composite score ranges and planned fields of study: Selected years, 1995 through 2009.” National Center for Education Statistics.Available online at / (accessed May 14, 2013). Standard normal table for proportion between values (Opens a modal) Finding z-score for a percentile (Opens a modal) Threshold for low percentile (Opens a modal) Basic normal calculations (Opens a modal) Practice. “2012 College-Bound Seniors Total Group Profile Report.” CollegeBoard, 2012.“The Use of Epidemiological Tools in Conflict-affected populations: Open-access educational resources for policy-makers: Calculation of z-scores.” London School of Hygiene and Tropical Medicine, 2009.“Blood Pressure of Males and Females.” StatCruch, 2013.The z-scores are –3 and +3 for 32 and 68, respectively. The values 50 – 18 = 32 and 50 + 18 = 68 are within three standard deviations of the mean 50. The value of a z-score has two parts: the sign (positive or negative) and the magnitude. Therefore, about 99.7% of the x values lie between –3σ = (–3)(6) = –18 and 3σ = (3)(6) = 18 from the mean 50. If the data sets have different means and standard deviations. p0.24825 By interpolation,we can get the z score for p 0. About 99.7% of the x values lie within three standard deviations of the mean. Answer (1 of 5): We can find out from the standard normal table as follows: The p-values for the Z scores are as follows: Z.
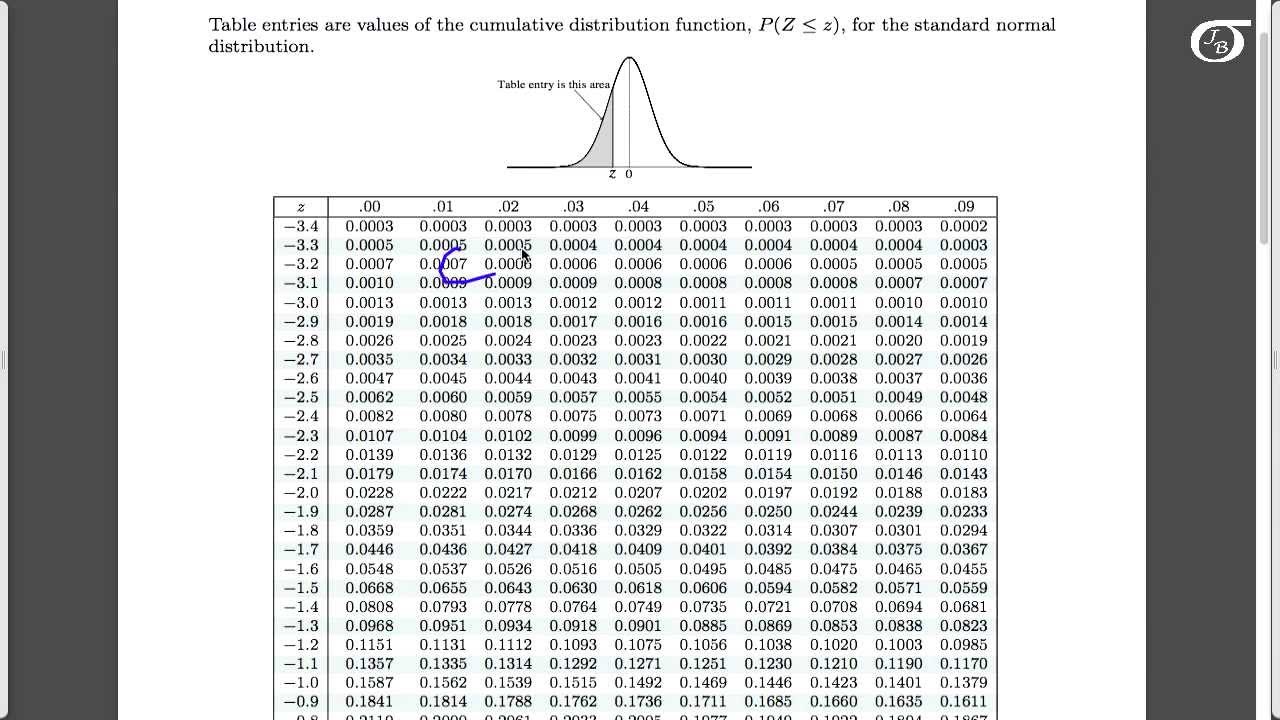
The z-scores are –2 and +2 for 38 and 62, respectively. The values 50 – 12 = 38 and 50 + 12 = 62 are within two standard deviations from the mean 50.

The values 50 – 6 = 44 and 50 + 6 = 56 are within one standard deviation from the mean 50. About 68% of the x values lie within one standard deviation of the mean.Suppose x has a normal distribution with mean 50 and standard deviation 6. \(X = 157.44\) cm, The \(z\)-score(\(z = –2\)) tells you that the male’s height is two standard deviations to the left of the mean. If \(X\) is a normally distributed random variable and \(X \sim N(\mu, \sigma)\), then the z-score is:


 0 kommentar(er)
0 kommentar(er)
